A customary individual can evaluate reinforcement as a singular amount. We see numerous individuals gauge reinforcement as a level of solid volume, for example, 2% or 1.5% of solid volume. In any case, as a development proficient you shouldn't gauge rebar amount as a percent of solid volume. You should appraise that as appeared in the basic drawing.
Evaluating rebar amount is simple. All you need to get the cutting length for each kind of bar in the beam. In this post, we will talk about how to appraise beam reinforcement from the drawing. We'll utilize the standard ideals as an auxiliary drawing of the beam.
For assessing beam reinforcement, you will first need to realize which kinds of bars are accessible in the beam. From the ideal plan we have discovered the accompanying information:
You will likewise require the accompanying information to appraise the beam reinforcement -
You can get this information from the overall notes sheet of auxiliary drawing. So, now we have enough information to gauge the beam reinforcement. Let us start the estimate now.
The quantity of steel shifts in a few auxiliary components since load (pliable force) involved by different parts are extraordinary. Load (elastic force) on beam is more than load on slab somewhat. Thusly, steel quantity in beam is hardly more prominent than slab and other basic parts.
Subsequently,
Please note that by and large, it isn't prescribed to surpass 4% (314kg/m^3) reinforcement in Column as it will be entangled to pour concrete and minimal it".
To acquire the ideal quantity of steel the parts ought to be structured based on standard codes rules.
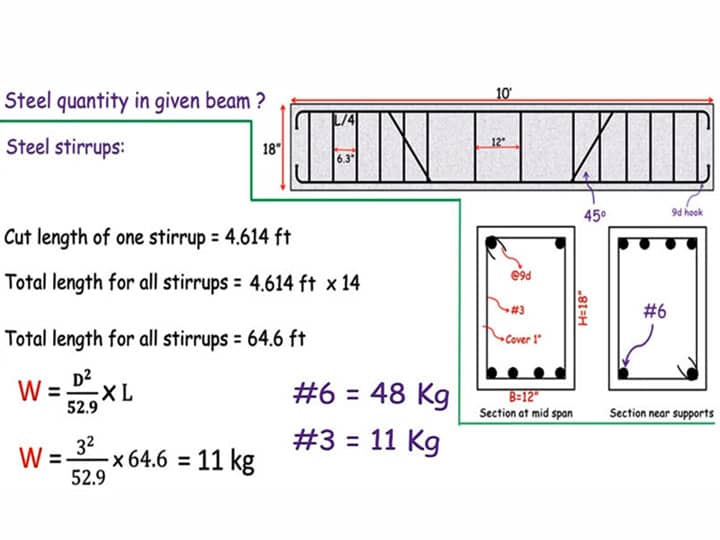
In this development video instructional exercise introduced by the famous specialist, S.L.Khan, you will figure out how to the measure the quantity of steel in a beam with length 10 feet and profundity 18 inches. The element of snare in two principle bars is taken as 9d. Two twisted up bars are given in beam a heavenly attendant of 45 degree with the flat lines.
There are two areas in the beam. One is situated at mid-range and other is found adjoining the backings. The above auxiliary drawings are presented by the originator. The quantity assessors can decide the quantity of steels from these auxiliary drawings.
At first, it is needed to decide the quantity of steel for straight fundamental bars. There are absolute 5 bars like two bowed up bars and four straight bars.
The complete cut length of bars will be resolved with the accompanying recipe:
Apply the accompanying formula to get the cutting length of the top longitudinal bar.
Cutting Length of top longitudinal bar is,
= Length of beam – 2 × clear cover + 2 × bend length – 2 × bend deduction length + lap length
Now, Length of beam: 20″ + (22′-8″) + 20″ + (8′-4″) + 20″ = 36′ (from above)
Clear cover: 1½"
Bend length: 12D = 12 × 20 = 240 mm, state 9½"
Bend deduction length: Bend deduction length for 90° bend is equivalent to multiple times of bardia= 2 × 20 mm = 40mm = 1½"
Thus, the cutting length of the top longitudinal bar is,
= 36′ – 2 × 1½" + 2 × 9½ – 2 × 1½" + 0
= 37′-1″.
There are Three quantities of the top longitudinal bar in the above picture. So, the complete length of the top longitudinal bar is,
= 3 × (37′-1″)
= 111′-3″.
We know the full length of a strengthening bar is about 40′. The length of a top longitudinal bar, we are assessing, doesn't surpass the length of a stocked bar. So, you don't need to include lap length.
The recipe for computing the cutting length of the base longitudinal bar is equivalent to the equation for the top longitudinal bar. So, the length is additionally equivalent to T1. That is 37′-1″.
Therefore, the absolute length of the B1 bar is,
= number of B1 bar × cutting length of a B1 bar
= 3 × (37′-1″)
=111′-3″.
Computing cutting length of additional top bar follow the accompanying equation:
Cutting length of Et1 = expanded length from support + width of support – clear cover + bend length – bend deduction length
Expanded length from support: 7′-5″
Width of support: 20″
Clear cover: 1½"
Bend length: 9½"
Bend deduction length: 1½"
Therefore, the cutting length of Et1 is,
= (7′-5″) + 20″ – 1½" + 9½" – 1½"
= 9′-7½"
There are two quantities of Et1 bar appeared in the drawing.Sothe absolute length of Et1 is,
=2 × (9′-7½")
= 19′-3″
Expanded length from support: 7′-5″
Width of support: width of support for Et2 ought to be the width of support2 + separation somewhere in the range of support2 and support3 + width of support3 = 20″ + (8′-4″) + 20″ = 11′-8″
Clear cover: 1½"
Bend length: 9½"
Bend deduction length: 1½"
In this way, cutting length of Et2 = (7′-5″) + (11′-8″) – 1½" + 9½" – 1½"
= 19′-7½"
All out length of Et2 = 2 × (19′-7½")
= 39′-3″
Cutting length of the additional base bar is,
=Distance between support – 2 × separation between additional base bar and closest support
= (22′-8″) – 2 × (2′-10″)
= 17′
The absolute length of the additional base bar is,
= 2 × 17′ (there are 2 bars for Eb appeared in the picture above)
= 34′
Be that as it may, steel fortifying bars are estimated in kilograms in the market. So, you need to change over the bar length to kilograms. Unit weight of 10 mm ø bar is 0.188 kg/ft and 20 mm ø bar is 0.75 kg/ft. So, the reinforcement required for our model beam,
Note: When you need to buy strengthening bar for the beam you should include 5% more with your evaluated amount as wastage.