Load transfer mechanism in reinforced cement concrete (RCC) structures are a truly intriguing matter. The loads of a floor fall totally on the floor slab. They are transferred to the beams, then to the columns, and finally to foundation. Today, we will do a comparative analysis of slab to beam load transfer.
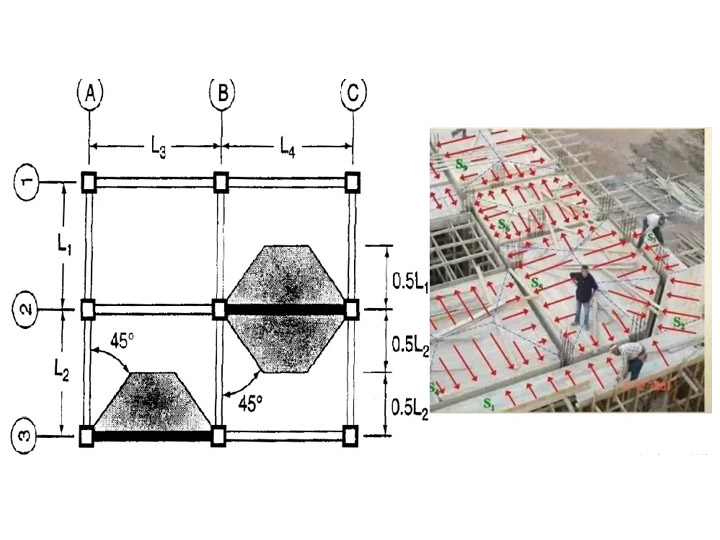
The forces acting on a slab are expressed as slab pressure loads, which are told in terms of kN/m2. However, when these loads are transferred to the beams supporting the slab, they morph into what we call line loads on beams, given in kN/m. This transfer has to be uniform on all sides (unless you have designed it specially for skewed loads) or else the flooring may crack, or worse.
Reynolds and Steedman (2005) present some very useful formulas to represent uniformly distributed slab loads transferred to beams. These formulae are great for analyzing the load transfer system from a two-way or one-way slab to its supporting beam.
The formulas are as follows:
We can take three different approaches to do a comparative analysis of slab to beam load transfer. These are:
Now let us look at each method one by one, each once for a one-way slab and a two way slab.
One-way slab
Data given:
Therefore,
Aspect ratio, k
Long span beam
Short span beam:
Long span beam:
Short span beam:
Load on long span beam
Load on the short span beam
So, we can see that in the one-way slab system, in the longer side, the finite element analysis and yield line analysis methods give quite similar results. But our manual calculation has overestimated the bending moment and shear forces.
In the short span direction, both the yield line method and manual method underestimates the loads transferred. However, the manual calculation gives quite good results for bending moments that can be used for design.
Two-way slab
Data given:
Therefore,
Aspect ratio, k
Long span beam
Short span beam:
Long span beam:
Short span beam:
Load on long span beam
Load on the short span beam
Now, in the case of two-way slabs, our observations are obviously not much different. The bending moment and shear forces are quite similar in automated Staad Pro methods (1 and 2). Again, manual analysis overestimates the slab loads transferred to the beam in the long span.
Whereas in the short span, yield line method falls short of expectation but manual method gave came very close to the automated finite element analysis. This is a dependable result and thus can be used in design. However, the sagging moment in the long span needs to be redistributed by 10%.