Bent Up Bar in Slab Cutting Length Calculation

If you are a civil engineer or a site engineer, it is essential for you to be able to calculate the cutting lengths of the reinforcement bars inside every load-bearing member. The same applies for the bent up bar in slab cutting length calculation. Today, we will try to explain it using a live example.

A bent up bar in slab is also called a crank. It is extremely important since it is used as the main reinforcement in the floor slab. It is provided in the bottom side of the slab, in the shorter side of the span. The main purpose of providing this bent up bar or crank is to transfer both the dead and live load of the slab to the beam. This load is then carried from the beam to the columns, from the column to the footing, and from the footing to the ground soil.

Why do you need to calculate bent up bar in slab

When you don’t have to deal with a much large construction area, the detailing of reinforcements in slabs can be done by bar bending schedules, by the person in charge of it. Those in charge of BBS or the bar benders can take care of the reinforcement detailing.

However, this method may not be perfect because the bar benders may not be vigilant in taking account of the cranks and bends, though they will give out some amount of cutting length. They might give some extra cutting length, but that will almost certainly not be enough for your bending requirement.

To remedy this problem, all site engineers responsible for considerable floor areas need to be capable of calculating the cutting length of bent bars in slabs on their own, independent of bar benders. This article will try to explain this in detail, to help you in working out the nuts and bolts of the bar cranking process. Please pay attention because it can be complicated.

Calculation of the bent bar in slab

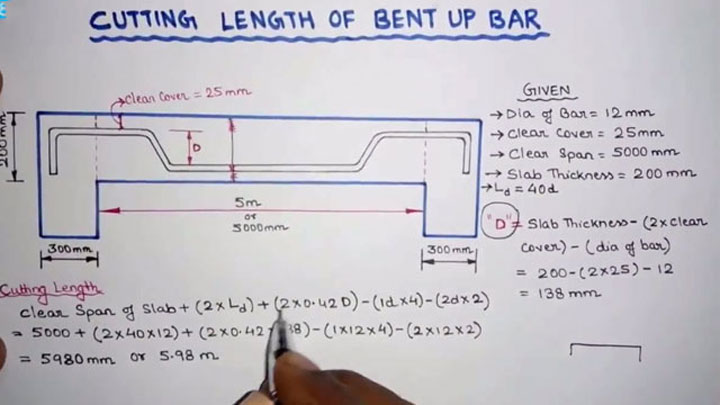
Let us say that the scenario has the following dimensions of things:

• Diameter of the bar = 12 mm
  
• Clear Cover = 25 mm
• Clear Span (L) = 8000
• Slab Thickness = 200 mm
• Development Length(Ld) = 40d

Now that we have the given data, we can figure out the cutting length of the bent bar in the given slab.

Process of computing the cutting length of bent bar in slab

Formula:
Cutting Length = Clear Span of Slab + (2 x Development Length) + (2 x inclined length) – (45° bend x 4) – (90° bend x 2)
In this scenario,
Inclined length
= D/(sin 45°) – dD/ (tan 45°)
= (D/0.7071) – (D/1)
= (1D – 0.7071D)/0.7071
= 0.42 D

Now, in this scenario, there are four 45° bends at the inner side and two 90° bends in the system.
We take 45 ° = 1d and 90 ° = 2d
So, Cutting Length = Clear Span of Slab + (2 X Ld) + (2 x 0.42D) – (1d x 4) – (2d x 2)
Where,

• d denotes Diameter of the bar.
• Ld denotes Development length of the bar.
• D denotes Height of the bending bar.

With the above formula, all values are established exclusive of D.

Therefore, now we just need to find out the value of D.

Here, D = Slab Thickness – (2 x clear cover) – (diameter of bar)
= 200 – (2 × 25) – 12
= 138 mm

Using the values found out in the computations above in the formula, we get,

Cutting Length = Clear Span of Slab + (2 x Ld) + (2 x 0.42D) – (1d x 4) – (2d x 2)
= 8000 + (2 x 40 x 12) + (2 x 0.42 x 138) – (1 x 12 x 4) – (2 x 12 x 2)
This calculates out to:
Cutting Length = 8980 mm or 8.98 m.

We hope this was useful for your civil engineering work! Please let us know what you think using the comment section below. We would love to know your thoughts and suggestions. Till next time, happy building!